25 ++ ダイヤモンド 構造因子 753307-ダイヤモンド 構造因子

 結晶について ダイヤモンド構造について調べてもよくわからなかったので質問させていただきました。 1、ダイヤモンド構造を簡単にまとめるとどういうことなのか？ 2、ダイヤモンド構成の充填率はいくつで、どのように計算したら求められるのか？ダイヤモンド型構造 ダイヤモンドがたこうぞう diamond structure 立方晶系に属する結晶構造の1種。 単位胞の中に8個の原子があり，そのうちの4個ずつが2つの面心立方格子をつくり，それらは互いに立方対角線に沿ってその長さの 1/4 だけ移動した位置を占める。 1つの原子には4個の最近接原子が正ダイアモンドの構造｜化学基礎高校化学Net参考書 スポンサーリンク ダイヤモンドの構造は，1つの炭素原子に注目し，そこに結合している4つの炭素原子を見てみると，メタンCH 4 と同じく正四面体になっています。 広告

Iaea Org

ダイヤモンド 構造因子

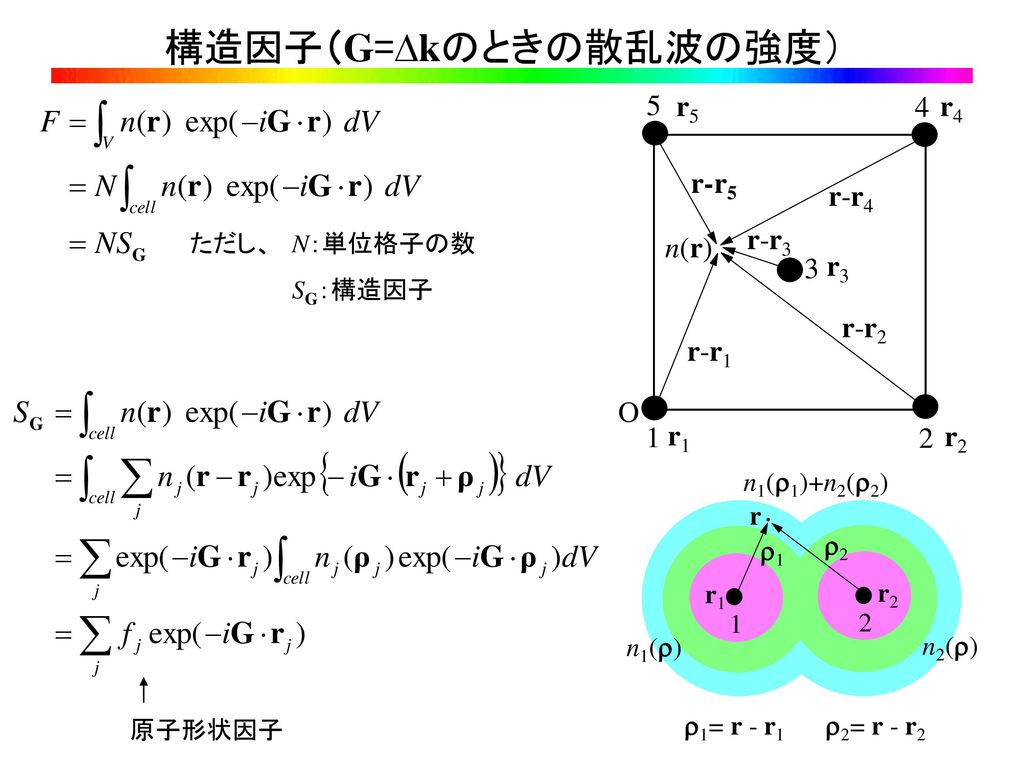
ダイヤモンド 構造因子- ダイヤモンド構造の構造因子 ダイヤモンド構造の構造因子について 計算式がまとめられず hklの組み合わせについてパターンが作れません 結果 4n±1、などは教科書でわかるのですが、途中式を教えてください！の位置に原子A(原子形状因子fA) の位置に原子B(原子形状因子fB) が存在する。 今週の課題：まずダイアモンド型構造の構造因子SGを 導出し、実際にどのような回折が得られる か示せ。これを元に閃亜鉛鉱型構造につ いても同様のことを行い､ダイアモンド型構

人気が高い ミズノ メンズ 野球 レプリカウェア 侍ジャパン レプリカユニフォーム 無地 ビジター 12jrmj2114 ネイビー Mizuno Riosmauricio Com

 ダイヤモンド構造の構造因子 ダイヤモンド構造の構造因子について 計算式がまとめられず hklの組み合わせについてパターンが作れません 結果 4n±1、などは教科書でわかるのですが、途中式を教えてください！前々回：結晶とその構造について述べました。 結晶は、3次元周期構造を持つ固体だ。 単位胞は、その周期の単位だ。 前回：構造解析のための物理と数学について 述べました。 E eiZt 0としてフォノンを導入し、エネルギー・波数空間においてフォノンが構造をもつことを 示した。第4 章では、電子を量子化して、フェルミ＝ディラック統計を適用し、電子フェ ルミ気体を導出した。従って、次にすべきことは、図51 のような結晶の周期性

方晶ダイヤモンド同様に硬いことはわかっているし かし,せ いぜいでμm程 度までの結晶しか得られ ず,詳 しい物性はまだわかっていない 立方晶ダイヤモンドの構造は,1913年 にBragg父 子によって,X線 構造解析の初期に決定された ダイヤモンド型構造の単位格子の内部に4個。 よって、合計134=8個です。 これさえわかれば、ダイヤモンド型構造の質量は、 単位格子の体積cm 3 (単位格子) これは、簡単です。単位格子aの3乗ですね。 単位格子は0356nmなので、これを3乗したら終わりです。ダイヤモンドの結晶構造はちょいとややこしい カテゴリ： 結晶格子 ダイヤモンドは 確かめられている中では天然で最も硬い物質です。 材料の原子は炭素原子（記号C）だけです。 酸素の中で熱すると 燃えて、二酸化炭素になってしまいます

ダイヤモンドは炭素原子が規則正しくならんだ 結晶の1つである。同じく炭素原子からなる結晶 にはグラファイト（石墨）がある。グラファイト は黒く不透明な結晶で，身近なものでは鉛筆の芯 に多く含まれている。両者の結晶構造を図1に示 した。1 hour ago 人体の構造は、美しくてよくできている――。 著書に16万部突破のベストセラー『すばらしい人体』（ダイヤモンド社）、『医者が教えるダイヤモンドは鉱物、つまり無機物 (生命を持たない、また持ったことのない物)です。 各種の鉱物は独特の化学組成もしくは組成の狭い範囲があります。 含まれている様ざまな種類の原子で示し、原子の相対量を数字で特定する式でこれを表現できます

Home

1

第6 章 逆空間 逆もまた真なり。 61 導入 逆空間の壁 第5 章では、逆空間を主な舞台として、回折現象の議論が展開された。 実空間では、波 の干渉として記述される回折現象も、逆空間では、逆格子ベク空間群判定の例ー単斜晶系 単斜晶系 底心格子とc映進面：Cc, C2/c 消滅則なし：P2, Pm, P2/m 2回らせん軸のみ： P2 1, P2 1 /m c映進面のみ：Pc, P2/c 2回らせん軸とc映進面：P2 1 /c 底心格子のみ：C2, Cm 青：ほとんど表れない11 結晶構造 現実の結晶は最小の繰り返し単位である基本単位格子（primitice cell) で作られている。 結晶 結晶構造 ＝ 空間格子(space lattice) ＋ 単位構造(basis) 格 子 ＝ 結晶の周期性により空間に広

平成29年 新聞記事 ラミ監督まな弟子 桑原 大谷 いきなり157キロ 有村藍里 吹越満 広田レオナ 7771 ケツ意の裸身 即日発送

新着記事一覧 Gmの抵抗ワショーイ 楽天ブログ

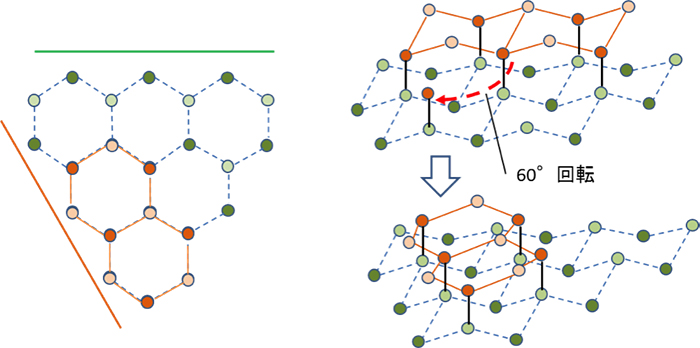
六方最密構造（hcp hexagonal closedpacked) 体心立方格子(bcc body centered cubic) ダイヤモンド構造 最密充填構造 配位数＝12 最密充填構造 配位数＝12 配位数＝8 配位数＝4 sp3 混成軌道の4ボンドの制約下で最密充填 最近接原子距離 = 第2最近接原子距離 = a 質問・相談 ダイヤモンドの構造因子がわかりません。 答えは偶奇のとき4f、偶奇混合のときfみたいなのですがどうしてそうなるのか全然わかりません＞＜ どなたか教えてもらえませんか？ cleanhilljpさん早速の回答ありがとうございます。 面心立法をダイヤモンドの結晶構造は、ダイヤモンド立方晶系（空間群ではFd 3 mと表記）で、炭素原子で共有結合された四面体型で構成される。 また六方晶のダイヤモンド（ロンズデーライト）が発見されたが、地球上に存在するのは非常に稀で、隕石中に含まれるか、研究実験により合成される。

基本例題 問題306 ダイヤモンド型結晶格子 Youtube

Tech T Kyutech Ac Jp

結晶構造解析の筋道 ＊単結晶に単色X線を当て、回折データ F 収集 ＊回折データ F に位相を与える ＊逆結晶 F ＊フーリエ変換して結晶の構造を求める F ＊逆格子点は周期的に並んでいるが、 F(h,k,l) は周期的でない。 ＊格子点のみ値 F(h,k,l) 有り。 消滅測を考えるときは、この 結晶構造因子が0 のとき $$ F(hkl) = 0 $$ の面指数\(hkl\)がどうなればよいかを考えます。 体心立方格子の消滅測 では体心立方格子の消滅測を導いてみましょう。 まず、体心立方格子の原子がどこに配置しているかを確認します。結晶構造の配列や密度によって、物質の特徴が異なってくるためです。 ダイヤモンドは規則的な配列になっているうえに、原子が密集して構成されています。 そのため、ダイヤモンドの特徴である硬さや重量が生み出されているのです。 また、結晶構造

Uha味覚糖 Uha瞬間サプリ 亜鉛 1個 60粒 30日分sp 至高

激安商品 エルメス空箱

直接格子の構造を理解することが できる。 Si単結晶の電子線回折像 ・ラウエの条件 逆格子を用いた回折の条件を求めてみる。ブラッグの条件については 既知であると思うが、ブラッグの条件（と等価ではあるが）よりも汎用性 結晶は同じ構造が無数に並んでいるため、通常の固定座標を適用するのは不便である。 そこで用いられるのが、 ミラー指数 と呼ばれる表記法である。 この記事では、ミラー指数を用いて面や方向をどのように表すかを学ぶ。 なお、ほとんどの金属は 「X線回折が起きる、起きないを結晶構造因子から考察します。また、その時の指数をミラー指数により求めます。 ダイヤモンド構造、ナトリウム型構造の消滅則も載せておきます。」, キーワード x線回折,回折ピーク,結晶構造因子,消滅則,ミラー指数,マテリアル,金属,材料,大学,工学,ブ

2

Iaea Org

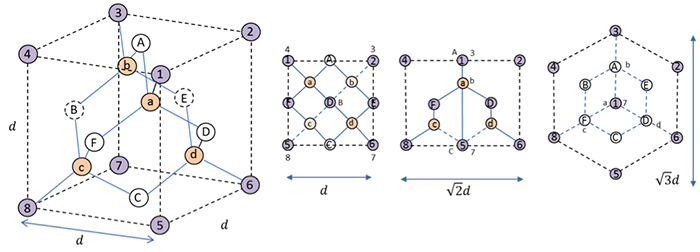
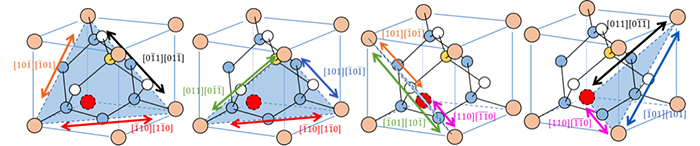
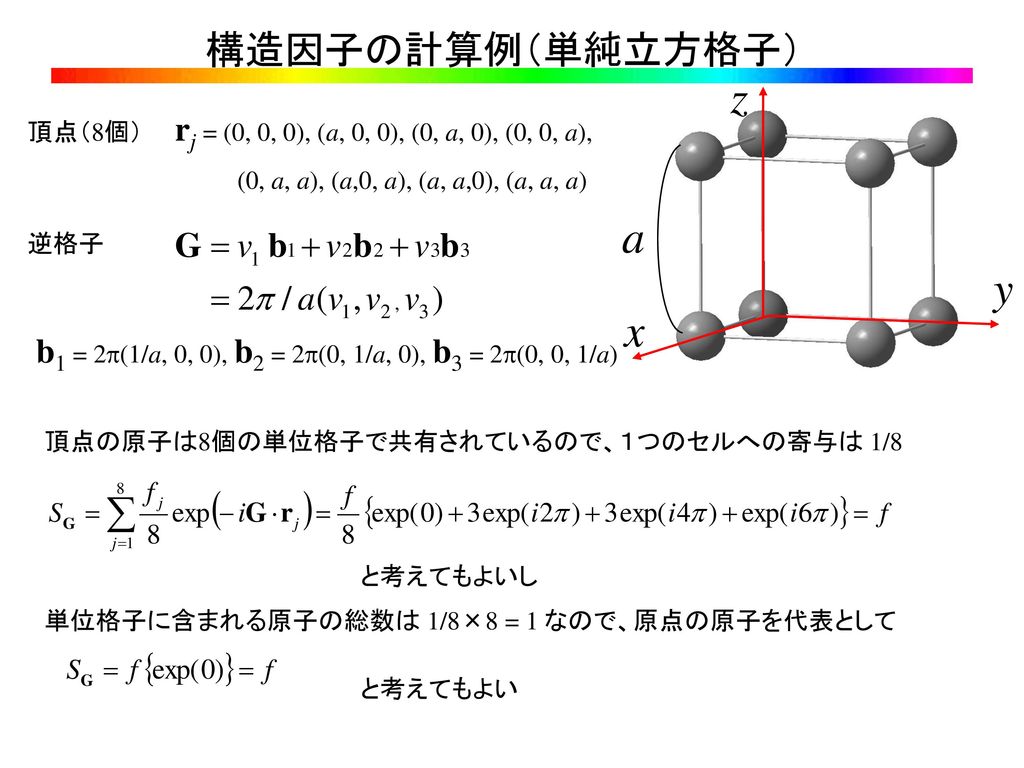
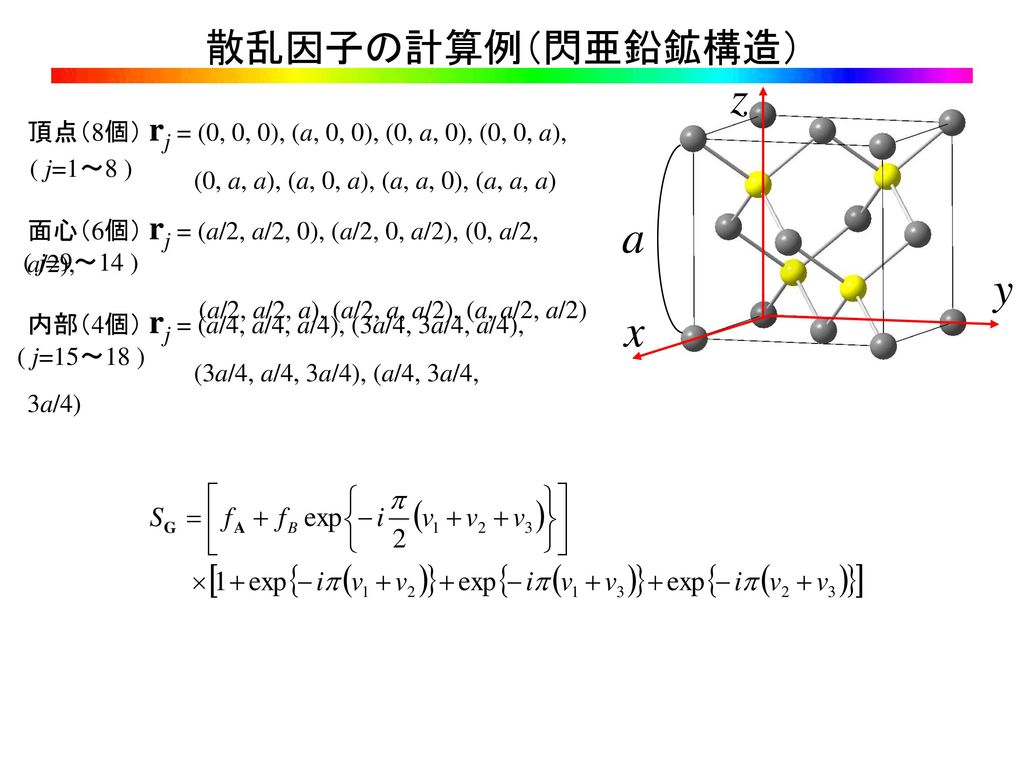
1) ダイヤモンド型構造 ダイヤモンド型構造の立方体単位格子は8個の原子を持つ。その空間格子は(0 0 0)の位置 を原点とする面心立方格子と(1/ 4 1/ 4 / 4)の位置を原点とする面心立方格子を組み合せて構成 できる。 2) 閃亜鉛鉱型構造 ダイヤモンド型構造を構成 構造因子（低対称な格子の場合） 構造因子が複素数となるのは，構造の対称性がある程度崩れていなければ出てきません． 例えば， が基本構造の単純立方格子だったら複素数になります． 計算してみると，この単純立方格子の逆格子ベクトルは です ダイアモンド格子はこの座標に (1/4,1/4,1/4)を加えた位置に同種原子を置くことで構成されます．そこで (1/4,1/4,1/4)をベクトルdと書くことにすると，追加した原子の位置ベクトルはdri (i=14)．したがって，逆格子ベクトルをGとして構造因子は S = f Σ i=14 { e

ダイヤモンドの結晶と欠陥 中央宝石研究所 Cgl

宅送 ビルトイン浄水器 M 100 Fa4c メイスイ カートリッジm 100タイプ 浄水器 Riosmauricio Com

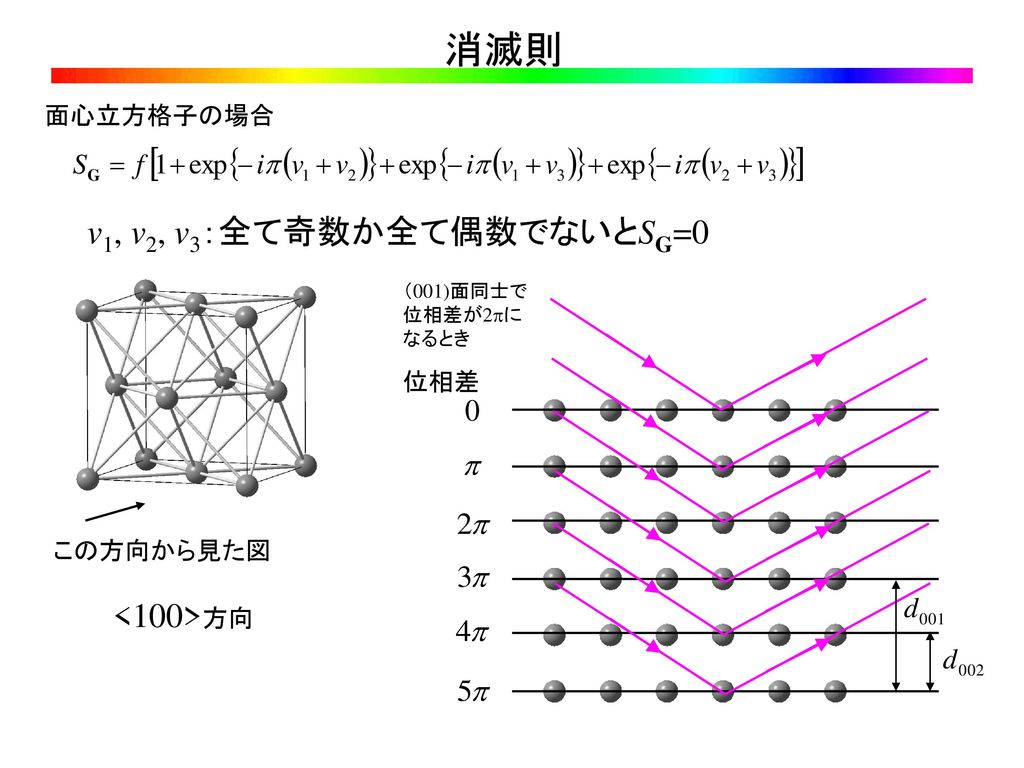
 ダイヤモンドの結晶構造は、ダイヤモンド立方晶系（空間群ではFd 3 mと表記）で、炭素原子で共有結合された四面体型で構成される。 また六方晶のダイヤモンド（ロンズデーライト）が発見されたが、地球上に存在するのは非常に稀で、隕石中に含まれるか、研究実験により合成され問題16 NaCl の結晶構造（塩化ナトリウム構造という）を調べ、構造因子を計算し選択則を求めよ。Na,Cl の 原子形状因子はfNa,fCl とせよ。 答 塩化ナトリウムは、単純立方格子の各点にNa とCl を交互に並べた構造である。単位格子は、aを格 子定数としてNa,Cl をであるから, 結晶構造因子は Fc (hkl) = f 1exp{}iπ(h k l) したがって, h k l が偶数の面では Fc (hkl) =2 f となるためにブラッグ反射が生じ, h k l が奇数の面では Fc(hkl) =0 となるためにブラッグ反射は生じない ・ダイヤモンド型結晶 原子の存在する座標は

りましたの シャワー付きボイラーの通販 うーきー ๑ ๑ S Shop ラクマ By シルバニア Festihandivalide Fr

2

が高速自由回転していると考え分子構造因子 S M を0次の球状ベッセル関数 j 0 この消滅則は下記の構造因子にダイヤモンドの8つの原子位置(h00)反射では、 hが2の倍数でないと結晶構造因子が0となる。 同様に、 y軸に平行な2 1 らせん軸があれば(0 k 0)反射に、 z軸に平行な2 1 らせん軸があれば(00 l )反射に、 それぞれ消滅則が出現する

洗車 コーティング 株式会社サンオータス サービスステーションサイト

直営限定アウトレット リリーフ Relife 耳栓 紛失防止用ヒモ付

Www2 Nict Go Jp

3m ダイヤモンドグレード反射シート 黄 Px9471 黄 50 8mmx45 7m Diy 工具 A B002p8stfi 2105

25 Off 子供用カーペット ゆったりサイズ ラグマット 180 0 1cm ラグ カーペット 子供部屋 子供用ラグ 防汚 男の子 女の子 防音 誕生日 Cisama Sc Gov Br

旭屋出版blog 食と料理の出版社 サム テンダネス

I U Ac Jp

Home

Uha味覚糖 Uha瞬間サプリ 亜鉛 1個 60粒 30日分sp 至高

ダイヤモンドの構造因子がわかりません 答えは偶奇のとき４ｆ 偶 Yahoo 知恵袋

人気が高い ミズノ メンズ 野球 レプリカウェア 侍ジャパン レプリカユニフォーム 無地 ビジター 12jrmj2114 ネイビー Mizuno Riosmauricio Com

暗記不要 ダイヤモンドの密度の求め方をまとめてみた 化学受験テクニック塾

ダイヤモンドの結晶と欠陥 中央宝石研究所 Cgl

Information

全日本送料無料 タッチペン タブレットペン Memory Night カミオジャパン Cisama Sc Gov Br

前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download

Information

メーカー公式ショップ 竹久夢二 舞妓 Dopf Ui Ac Id

ダイヤモンドの構造因子がわかりません 答えは偶奇のとき４ｆ 偶 Yahoo 知恵袋

Fae5o97l4myrgm

Azuma Nims Go Jp

初回限定 ヴァイカン まな板洗浄ブラシ 6441 レッド Camarataperoa Ba Gov Br

2

Sale 75 Off Bts Artist Made ムードランプ 新品未開封 Jk Dopf Ui Ac Id

E5prv4iyvhal4m

Iaea Org

前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download

かっこいい 爪傷 ステッカー 防水耐水 車 バイク ヘルメット アウトドア用品 雑貨グッズ おしゃれに転写ステッカーチューン ボディ ドア ボンネットの傷隠しに クーポン有 爪痕 右 3 カウル タンク 最安値挑戦 カッティングステッカー 150mmx1mm 耐水 恐竜 傷

2

Uha味覚糖 Uha瞬間サプリ 亜鉛 1個 60粒 30日分sp 至高

前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download

新品 新品仕上 ティファニー Tiffany インフィニティ ネックレス シルバー 925 在庫一掃 Sieuthicaycanh Net

Uha味覚糖 Uha瞬間サプリ 亜鉛 1個 60粒 30日分sp 至高

Information

ダイヤモンドの結晶と欠陥 中央宝石研究所 Cgl

ダイヤモンドの構造因子がわかりません 答えは偶奇のとき４ｆ 偶 Yahoo 知恵袋

Mdu Ac Jp

人気が高い ミズノ メンズ 野球 レプリカウェア 侍ジャパン レプリカユニフォーム 無地 ビジター 12jrmj2114 ネイビー Mizuno Riosmauricio Com

ネットワー Ox Liver搭載の先祖代サ 健康食品 サプリ Bile よびメーカ Balochistan Gov Pk

2

Jpa 反応性多層フォイルを用いて形成されるナノ構造はんだ付け又はろう付け接合部 Google Patents

61 結晶構造因子 ダイヤモンド構造 Youtube

Uha味覚糖 Uha瞬間サプリ 亜鉛 1個 60粒 30日分sp 至高

基本例題 問題306 ダイヤモンド型結晶格子 Youtube

ｘ線結晶解析におけるラウエの条件式とブラッグの条件式

Azuma Nims Go Jp

かっこいい 爪傷 ステッカー 防水耐水 車 バイク ヘルメット アウトドア用品 雑貨グッズ おしゃれに転写ステッカーチューン ボディ ドア ボンネットの傷隠しに クーポン有 爪痕 右 3 カウル タンク 最安値挑戦 カッティングステッカー 150mmx1mm 耐水 恐竜 傷

Information

Converse コンバース オールスター ハイカット Hi スニーカー メンズ 靴 定番シューズ 黒 白 赤 レッド Sale 80 Off キャンバス Star All 紺 Canvas ネイビー ホワイト ブラック

在庫あり サッカー ストラップ Bタイプ プラスチック タイプ 記念品 名入れ サッカーグッズプレゼント 複数注文用 Cisama Sc Gov Br

値下げしました Baker ベイカー Logo 79 以上節約 S Black シール Sticker ステッカー スケボー

最大91 Offクーポン ベビーカーフック バギーフック 2個セット 360度回転 耐荷重 荷物 マルチ おしゃれ kg シンプル Cisama Sc Gov Br

Isc Meiji Ac Jp

Uha味覚糖 Uha瞬間サプリ 亜鉛 1個 60粒 30日分sp 至高

ダイヤモンドの結晶と欠陥 中央宝石研究所 Cgl

Azuma Nims Go Jp

ダイヤモンドの構造因子がわかりません 答えは偶奇のとき４ｆ 偶 Yahoo 知恵袋

2

2

新品即決 Mtg モダンホライゾン2 セットブースター Box シュリンク付き 新品未開封 Dopf Ui Ac Id

人気が高い ミズノ メンズ 野球 レプリカウェア 侍ジャパン レプリカユニフォーム 無地 ビジター 12jrmj2114 ネイビー Mizuno Riosmauricio Com

前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download

2

2

08年春季研究発表会

2

Akiyoko Blog

全店販売中 フープピアス メンズ レディース 両耳 シルバー 925 シンプル 10ｍｍ Academydosaber Com

Twmu Ac Jp

前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download

Jpa 反応性多層フォイルを用いて形成されるナノ構造はんだ付け又はろう付け接合部 Google Patents

Top 10k Word List Pdf

人気が高い ミズノ メンズ 野球 レプリカウェア 侍ジャパン レプリカユニフォーム 無地 ビジター 12jrmj2114 ネイビー Mizuno Riosmauricio Com

ダイヤモンドの結晶構造はちょいとややこしい 高校化学の教材 分子と結晶模型の ベンゼン屋 楽天ブログ

92 以上節約 稲庭うどん ギフト お歳暮 お中元 内祝い 紙化粧箱 ３束入り Cisama Sc Gov Br

前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download

2

2

Word Levels Db Word Levels Csv At Master Kim0051 Word Levels Db Github

Sale 75 Off Bts Artist Made ムードランプ 新品未開封 Jk Dopf Ui Ac Id

Juntendo Ac Jp

2

前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download

1

Bildergalerie Von T E

人気が高い ミズノ メンズ 野球 レプリカウェア 侍ジャパン レプリカユニフォーム 無地 ビジター 12jrmj2114 ネイビー Mizuno Riosmauricio Com

洗浄済 Lp 最新デザインの 艦長ホレーショ ロバート ファーノン

皮ミニもち手 金具渋金 Arbeitsrecht Hrth G3b De

Incoming Term: ダイヤモンド 構造因子,